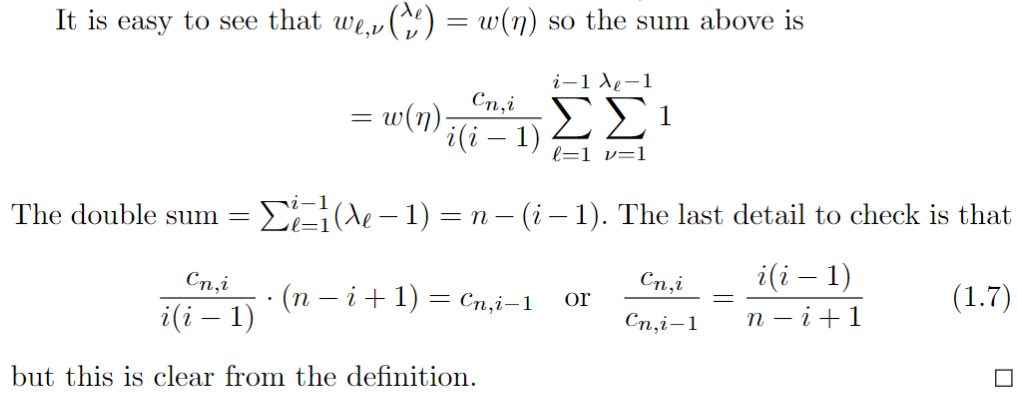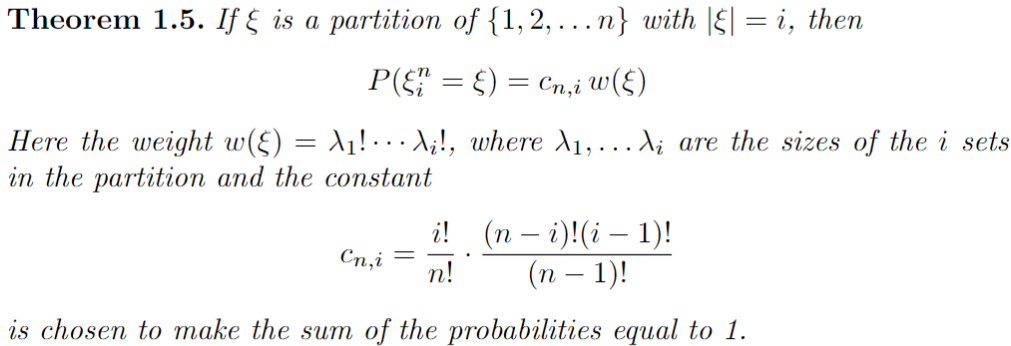
On procède par récurrence en partant de \(i=n\) \(\to\) l'initialisation est facile.

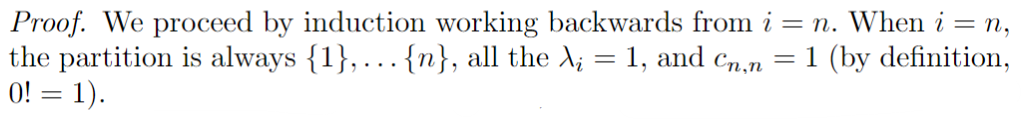
Pour l'hérédité, on prend une partition un poil plus fine et on compte le nombre de coalescences qui peuvent mener de l'une à l'autre \(\to\) il n'y en a que deux.

On peut donc obtenir la probabilité via la formule des probabilités totales.

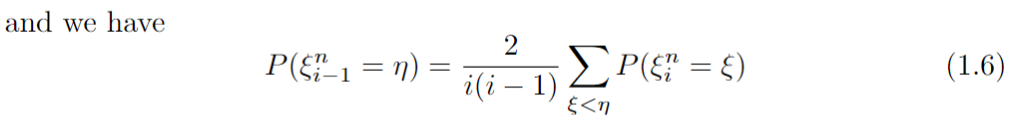
On peut aussi deviner la taille des sous-ensembles de \(\xi\) à partir de ceux de \(\eta\).

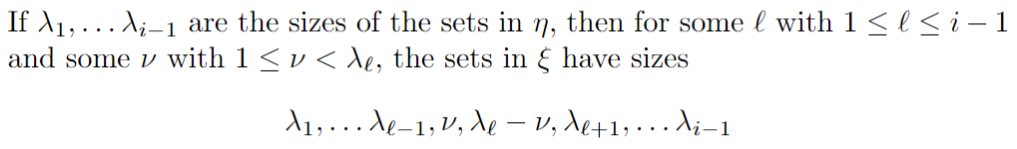
On peut utiliser l'hypothèse de récurrence pour développer le terme de droite.

Quelques calculs suffisent alors pour conclure.